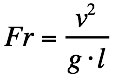Nov 7, 2001

Q: can we predict how walking will be in gravitational conditions different from Earth?
A: a simple equation introduced by a naval engineer, William Foude, in the 19th century to build ship models dynamically similar to the real ship comes to help. He realized that the exchange between kinetic and gravitational potential energy of bow waves was crucial in that comparison. Actually, the dimensionless speed he invented is also crucial in walking, where the same energy exchange occurs when considering the motion of the body centre of mass. The Froude equation allows to establish 1) dynamically equivalent walking speeds, at Earth gravity, for subjects of different stature, and 2) equivalent speeds, for subjects of the same stature, when walking in hypo- and hyper-gravitational conditions, as occurring in planets different from Earth. Data obtained from etherogravity simulations of walking confirm the validity of the Froude equation.
REF Minetti A. E. Walking on other planets. Nature 409: 467-469, 2001
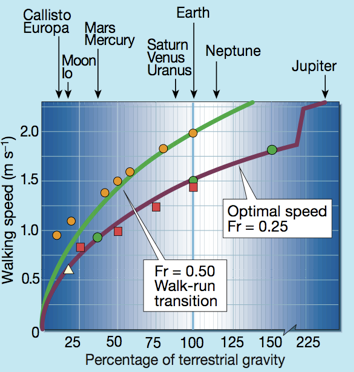
Walking speed as a function of gravity (expressed as a fraction of the terrestrial one). Thick parabola arcs represent the prediction of dynamic similarity according to the Froude number equation:
where l = 0.92 m (average leg length for adult males) and Fr has been set to 0.25 (maximum pendulum-like energy exchange, optimal walking speed on Earth) and to 0.5 (walk-run transition speed on Earth). The thin curve shows the physical limit to walking speed (Fr = 1.0) as imposed by the balance, in an inverted pendulum, between the centrifugal (m.v2.l-1) and the gravitational (m.g) force, necessary to maintain the contact with the ground. Square and open circle symbols refer to the measurements in reduced simulated gravity of the optimal walking speeds and walk-run transition speed, respectively. A previous estimate of speed reduction on the Moon is shown by the open triangle. Filled circles represent recent results of optimal speed obtained by using parabolic flight simulating hypo/hypergravity conditions.